Zad. 1. Czy każdy punkt każdego trójkąta ma sumę odległości od wszystkich wierzchołków mniejszą od połowy obwodu trójkąta? Uzasadnij!
Zad. 2. Ile jest par (x, y) liczb całkowitych ze zbioru {-2013, -2012, -2011, ..., 2012, 2013}, dla których [tex]x=\sqrt{x+y}[/tex]?
Zad. 3. Komputer losuje mniejszą od 2013 liczbę całkowitą dodatnią. Po ilu ruchach można mieć gwarancję, że się ją pozna, jeśli ruch polega na podaniu liczby, a komputer odpowiada, czy jest ona mniejsza, czy większa od szukanej, czy też jej równa?
Zadania marcowe okazały się trudne, część Ligowiczów argumentowała błędnie lub nieprecyzyjnie. Po 3 pkt przyznaliśmy jedynie Darii Bumażnik, Bartoszowi Czyżewskiemu i Klaudii Marcinkiewicz, a 2,5 pkt dostał Michał Turniak.
Na czele rankingu są zatem:
- z 16,5 pkt na 18 możliwych - Bartosz Czyżewski z Gim. w ZSO nr 1 w Jeleniej Górze i Michał Turniak z Gim. 49 we Wrocławiu,
- z 15 pkt - Igor Chełstowski z Gim. Dwujęzycznego przy I LO w Inowrocławiu,
- z 14 pkt - Tomasz Stempniak z Zespołu Szkół s. Salezjanek w Ostrowie Wlkp.,
- z 13,5 pkt - Daria Bumażnik z Gim. 1 w Jeleniej Górze i Klaudia Marcinkiewicz z Gim. 24 w Katowicach,
- z 11,5 pkt - Krzysztof Bednarek z Gim. 13 we Wrocławiu oraz Wojciech Wiśniewski z Gim. 3 w Giżycku.
Wszystkim gratulujemy!
Zad. 1. Nie - łatwo to sprawdzić, rozpatrując wierzchołek lub środek ciężkości trójkąta równobocznego (suma odległości wynosi wówczas odpowiednio 2a lub a√3 (gdzie a to długość boku), czyli w obu wypadkach więcej niż połowa obwodu).
Zad. 2. Z postaci równania widać, że x i x+y muszą być nieujemne. Przy takich założeniach mamy równanie równoważne: y=x(x–1), czyli rozwiązań jest tyle, ile spośród iloczynów 0·(-1), 1·0, 2·1, 3·2, ..., 2013·2012 jest w danym zbiorze. (x+y jest wówczas nieujemne "automatycznie"). 45·44 < 2013 < 46·45, więc odpowiedzią jest 46.
Zad. 3. W jednym ruchu można ustalić jedną z trzech kolejnych liczb (pytając o środkową), zatem w dwóch ruchach - jedną z siedmiu (po zapytaniu o środkową albo trafimy, albo zostajemy przy trzech możliwych, co załatwiamy kolejnym pytaniem), w trzech rundach - jedną z 15 itd. W dziewięciu pytaniach da się ustalić jedną z 1023 liczb, a w dziesięciu - jedną z 2047, odpowiedzią jest zatem 10 (ściślej: 10 lub więcej).




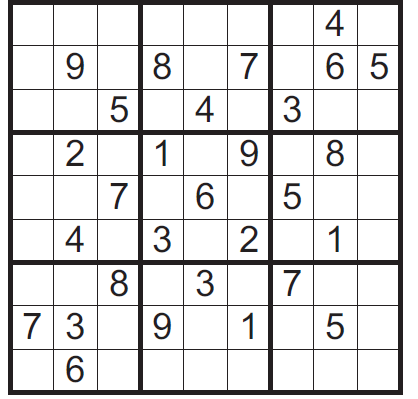
 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.

Brak zgody
Nie zgadzam sie z odpowiedzią do zadania 2. Przecież x może być liczbą ujemną, ponieważ (-2)2 wynosi 4. Zatem pierwiastek kwadratowy z 4 to zarówno 2 jak i (-2), więc rozwiązań będzie 90.
Pierwiastki parzystych stopni
Matematycy umówili się (można powiedzieć, że dla wygody), że pierwiastkiem kwadratowym z danej liczby jest taka liczba NIEUJEMNA, której kwadrat daje daną. (Podobnie jest z pierwiastkami dowolnych stopni parzystych). Zatem pierwiastek arytmetyczny z 4 to zawsze 2. Natomiast w algebrze, gdy rozwiązujemy równanie x2=4, podajemy oba pierwiastki tego równania, czyli √4 i (-√4), co daje liczby 2 i (-2).