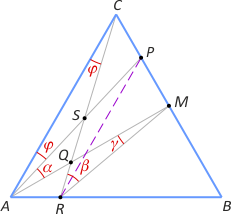
Zad. 1. Niech M oznacza środek boku BC w trójkącie równobocznym ABC. Na odcinkach CM i AB obrano punkty odpowiednio P i R takie, że |AR| = |CP|. Oblicz sumę miar kątów AMR, CRM i PAM.
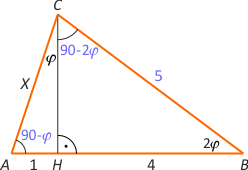
Zad. 2. Niech CH oznacza wysokość w trójkącie ABC. Wiedząc, że |AH|=1, |HB|=4 oraz że kąt B jest dwa razy większy od kąta ACH, oblicz długość AC.
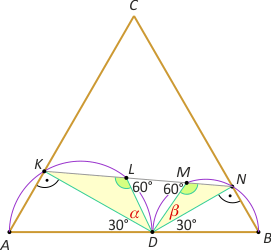
Zad. 3. Na boku AB trójkąta równobocznego ABC obrano punkt D (różny od śrdodka boku), a następnie na odcinkach AD i DB jako na średnicach zbudowano okręgi, które przecięły boki AC i BC odpowiednio w punktach K i N. Prosta KN przecina wtórnie te okręgi w punktach L i M (przy czym L leży między K i M). Wykaż, że |LM|2 = |KL|·|MN|.
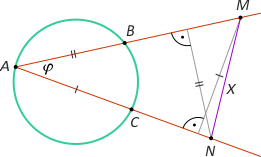
Zad. 4. (wolna amerykanka) Dany jest okrąg o promieniu R i dwie jego cięciwy AB i AC. Na prostej AB obrano punkt M, którego odległość od prostej AC równa jest |AC|, a na prostej AC obrano punkt N, którego odległość od prostej AB jest równa |AB|. Oblicz długość MN.
W tym miesiącu za zadania 1-3 punkty otrzymali:
30 - Iwona Gruszecka (nauczycielka w CLV LO Warszawa), Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia), Marzena Wąsiewicz (nauczycielka z Kajetan) oraz Szymon Kaźmierowski (nauczyciel z Elbląga),
10 - Janusz Wieczorek (emerytowany nauczyciel z Sandomierza).
Za zadanie 4 po 10 pkt. otrzymali: Iwona Gruszecka, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Mikołaj Popek, Tadeusz Porzucek, Marzena Wąsiewicz, Szymon Kaźmierowski, oraz Szymon Meyer (analityk danych z Dziewkowic).
Gratulujemy!
Zad. 1. Łatwo zauważyć, że czworokąt ARPC jest trapezem równoramiennym (dlaczego?). Oznaczmy miary kątów jak na rysunku. Zauważmy, że β+γ = |∡AQR| = α+|∡ASQ| = α+2φ, a stąd α+β+γ = 2(α+φ) = 2·30° = 60°.
Zad. 2. Zauważmy, że |∡C| = 90°–φ = |∡A|, skąd |BC|=5. Z twierdzenia Pitagorasa otrzymujemy x2–1 = 25–16 i ostatecznie x = √10.
Zad. 3. Wystarczy wykazać prawdziwość proporcji |LM|:|MN| = |KL|:|LM|. Czworokąty ADLK i DBNM są wpisane w okrąg, a stąd |∡DLM| = |∡LMD| = 60°, co oznacza, że trójkąt DNL jest równoboczny. Zauważmy, że 60° = α + |∡DKL|, a z drugiej strony z sumy kątów w czworokącie ABNK mamy |∡DKL| + |∡MND| = 60°, co oznacza, że |∡MND| = α i dalej |∡DKL| = β. Z podobieństwa trójkątów KDL i DNM przy uwzględnieniu, że |DM|=|LM| mamy tezę.
Zad. 4. (wolna amerykanka) Wobec założenia o przystawaniu zaznaczonych odcinków otrzymujemy sinα = |AC|:|AM| = |AB|:|AN|, skąd |AM|:|AN| = |AC|:|AB|, co oznacza, że trójkąty ACB i AMN są podobne (z cechy bkb) w skali k=sinα, zatem k = |BC|/x = 2Rsinα = sinα, skąd x = 2R.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
